| Non-Rationalised NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
| Content On This Page | ||
|---|---|---|
| Example 1 & 2 (Before Exercise 5.1) | Exercise 5.1 | Example 3 (Before Exercise 5.2) |
| Exercise 5.2 | ||
Chapter 5 Introduction To Euclid's Geometry
This section delves into the solutions for Chapter 5, titled "Introduction To Euclid’s Geometry." It serves as a crucial exploration into the very foundations of geometry as a structured field of mathematics. Unlike chapters that might focus heavily on algebraic manipulation or numerical problem-solving, this chapter, and consequently its solutions, prioritizes the understanding of logical structure, historical context, and the fundamental building blocks laid down by Euclid of Alexandria over two millennia ago. The solutions guide learners through Euclid's seminal work, "Elements," focusing intently on his methods, specifically his use of definitions, axioms (or common notions), and postulates. These three components collectively form the bedrock of the deductive system not just for geometry, but as a model for rigorous mathematical reasoning that has influenced thought for centuries.
The solutions meticulously clarify Euclid's approach, starting with his definitions. Euclid attempted to define fundamental geometric concepts such as a point ("that which has no part"), a line ("breadthless length"), and a surface ("that which has length and breadth only"). While modern mathematics often accepts terms like point and line as undefined primitives, understanding Euclid's efforts provides valuable historical insight into the development of mathematical rigor. The solutions help differentiate between these foundational definitions and the propositions derived from them.
A central theme elaborated upon in the solutions is the critical distinction between axioms and postulates. Axioms, often referred to as common notions by Euclid, were considered self-evident truths applicable across all fields of knowledge, not just geometry. Examples include: "Things which are equal to the same thing are equal to one another" and "The whole is greater than the part." Postulates, conversely, were assumptions specific to the domain of geometry – fundamental statements accepted without proof, upon which geometric theorems would be built. The solutions carefully explain Euclid's five postulates:
- A straight line segment can be drawn joining any two points.
- Any straight line segment can be extended indefinitely in a straight line.
- Given any straight line segment, a circle can be drawn having the segment as radius and one endpoint as center.
- All right angles are congruent (equal to one another).
- The famous parallel postulate: If a straight line falling on two straight lines makes the interior angles on the same side, let's call them $\alpha$ and $\beta$, such that their sum is less than two right angles (i.e., $\alpha + \beta < 180^\circ$), then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles.
Particular attention is often given in the solutions to the fifth postulate due to its complexity compared to the first four and its profound implications. Its less self-evident nature led to centuries of attempts to prove it from the other postulates and axioms. The solutions frequently discuss its significance and may introduce Playfair's axiom, an equivalent formulation often found easier to grasp: "Through a given point not on a given line, exactly one parallel line can be drawn to the given line." Understanding this postulate is key to understanding the nature of Euclidean geometry itself. Exercises typically involve applying these foundational rules, determining if a statement relies on an axiom or a postulate, constructing simple proofs (like proving that two distinct lines intersect at most at one point), and appreciating the consistency and power of the axiomatic structure of geometry established by Euclid. The focus remains firmly on logical deduction and conceptual clarity.
Example 1 & 2 (Before Exercise 5.1)
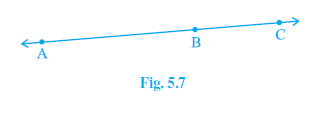
Example 1. If A, B and C are three points on a line, and B lies between A and C (see Fig. 5.7), then prove that AB + BC = AC.
Answer:
Given:
A, B, and C are three points on a line. Point B lies between points A and C.
To Prove:
$AB + BC = AC$
Proof:
In the given figure, we can see that the line segment AC is made up of two smaller line segments, AB and BC.
According to Euclid's Axiom 4, which states: "Things which coincide with one another are equal to one another."
If we place the line segment AB along AC, starting from point A, it will cover the portion of AC up to point B. If we then place the line segment BC along AC, starting from point B, it will cover the remaining portion from B to C.
The combination of the line segments AB and BC completely coincides with the line segment AC.
Therefore, based on this axiom, the length of the segment AC must be equal to the sum of the lengths of the segments AB and BC.
$AB + BC = AC$
Hence, proved.
Example 2. Prove that an equilateral triangle can be constructed on any given line segment.
Answer:
Given:
A line segment AB of any length.
To Prove:
An equilateral triangle can be constructed with AB as one of its sides.
Construction Required:
1. Using a compass, draw a circle with center A and radius AB.
2. Draw another circle with center B and radius BA.
3. Let the two circles intersect at a point C.
4. Join the points A and C to form the line segment AC, and join the points B and C to form the line segment BC.
5. $\triangle ABC$ is the required triangle.
Proof:
We need to prove that $\triangle ABC$ is an equilateral triangle, which means we need to show that all its sides are equal in length ($AB = BC = CA$).
AC = AB
(Radii of the same circle with center A) ... (i)
BC = BA
(Radii of the same circle with center B) ... (ii)
From (i) and (ii), we can see that $AB = AC$ and $AB = BC$.
According to Euclid's Axiom 1: "Things which are equal to the same thing are equal to one another."
Since both AC and BC are equal to AB, they must be equal to each other.
$AC = BC$
Therefore, we have established that:
$AB = BC = CA$
Since all three sides of $\triangle ABC$ are equal, it is an equilateral triangle.
This construction is possible for any given line segment AB, thus proving that an equilateral triangle can be constructed on any given line segment.
Exercise 5.1
Question 1. Which of the following statements are true and which are false? Give reasons for your answers.
(i) Only one line can pass through a single point.
(ii) There are an infinite number of lines which pass through two distinct points.
(iii) A terminated line can be produced indefinitely on both the sides.
(iv) If two circles are equal, then their radii are equal.
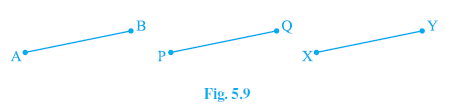
(v) In Fig. 5.9, if AB = PQ and PQ = XY, then AB = XY.
Answer:
(i) False.
Reason: Through a single point, infinitely many lines can be drawn in different directions. Imagine a point as the center of a wheel; infinitely many spokes (lines) can pass through it.
(ii) False.
Reason: Euclid's Postulate 1 states that "A unique straight line segment can be drawn from any point to any other point." This implies that given two distinct points, there is only one unique line that passes through both of them.
(iii) True.
Reason: This is a restatement of Euclid's Postulate 2: "A terminated line (which we understand as a line segment) can be produced indefinitely."
(iv) True.
Reason: If two circles are equal, they are congruent, meaning they have the same size and shape. If we superimpose one equal circle onto the other, their boundaries (circumferences) will coincide perfectly (Euclid's Axiom 4: Things which coincide with one another are equal to one another). The radius is the distance from the center to the circumference, which defines the size of the circle. Therefore, if the circles coincide, their radii must be equal.
(v) True.
Reason: This follows directly from Euclid's Axiom 1: "Things which are equal to the same thing are equal to one another." We are given $AB = PQ$ and $PQ = XY$. Since both AB and XY are equal to the same quantity (PQ), they must be equal to each other. Thus, $AB = XY$.
Question 2. Give a definition for each of the following terms. Are there other terms that need to be defined first? What are they, and how might you define them?
(i) parallel lines
(ii) perpendicular lines
(iii) line segment
(iv) radius of a circle
(v) square
Answer:
Yes, there are fundamental terms that need to be understood or accepted as undefined before defining the given terms. The most basic undefined terms in Euclidean geometry are usually taken as point, line, and plane. Additionally, concepts like distance, angle, lying on (a line/plane), between, and intersection are often used and need to be understood, even if not formally defined from scratch.
Assuming these basic terms and concepts are understood:
(i) Parallel lines: Two distinct lines lying in the same plane are said to be parallel if they do not intersect at any point, no matter how far they are extended.
Terms needed first: Line, Plane, Point, Intersect, Distinct.
(ii) Perpendicular lines: Two lines are said to be perpendicular if they intersect each other at a right angle (an angle measuring 90 degrees).
Terms needed first: Line, Intersect, Angle, Right Angle.
(iii) Line segment: A part of a line consisting of two distinct points on the line (called endpoints) and all the points lying between them.
Terms needed first: Line, Point, Endpoint, Between, Distinct.
(iv) Radius of a circle: A line segment connecting the center of a circle to any point on the circle's circumference. (The term 'radius' is also used for the length of this line segment).
Terms needed first: Circle, Center, Point, Line segment, Circumference (boundary of the circle).
(v) Square: A quadrilateral (a four-sided polygon) that has all four sides equal in length and all four interior angles equal to right angles (90 degrees).
Terms needed first: Quadrilateral, Polygon, Side, Length, Equal Length, Angle, Right Angle.
Possible Conceptual Definitions for Foundational Terms:
- Point: Represents a location but has no size or dimension. (Undefined)
- Line: A straight, one-dimensional figure having no thickness and extending infinitely in both directions. (Undefined)
- Plane: A flat, two-dimensional surface extending infinitely far. (Undefined)
- Intersect: To cross or meet. Two lines intersect if they share a common point.
- Angle: The figure formed by two rays sharing a common endpoint (vertex).
- Right Angle: An angle that measures 90°.
- Circle: The set of all points in a plane equidistant from a given point called the center.
- Quadrilateral: A polygon with four sides and four vertices.
Question 3. Consider two ‘postulates’ given below:
(i) Given any two distinct points A and B, there exists a third point C which is in between A and B.
(ii) There exist at least three points that are not on the same line.
Do these postulates contain any undefined terms? Are these postulates consistent? Do they follow from Euclid’s postulates? Explain.
Answer:
Undefined Terms:
Yes, these postulates contain undefined terms. The fundamental undefined terms are point and line. The concept of a point being "in between" two other points on a line is also usually taken as an undefined relation or needs definition based on distance/order, which is not provided by Euclid's basic framework.
Consistency:
Yes, these postulates are consistent. They describe different aspects of points and lines and do not contradict each other. Postulate (i) talks about the nature of points on a single line (suggesting density), while Postulate (ii) talks about the existence of points outside a single line (ensuring space is not just one line). It's possible for both to be true simultaneously.
Following from Euclid's Postulates:
No, these postulates do not directly follow from Euclid's five postulates.
- Postulate (i) implies that between any two points on a line, there's another point. Repeated application suggests infinitely many points on a segment. This property relates to the density or completeness of the line, which is an assumption made in modern geometry but is not explicitly stated or derivable from Euclid's five postulates.
- Postulate (ii) states that not all points lie on the same line; i.e., non-collinear points exist. This ensures that the geometry being considered is at least two-dimensional. While Euclid's geometry clearly deals with figures in a plane (like triangles and circles), his five postulates don't explicitly state this requirement for points. It's generally considered a necessary additional axiom for plane geometry.
Therefore, these are additional assumptions that are consistent with Euclid's system but not consequences of his original five postulates.
Question 4. If a point C lies between two points A and B such that AC = BC, then prove that AC = $\frac{1}{2}$AB. Explain by drawing the figure.
Answer:
Given:
A point C lies on the line segment AB such that it is between A and B.
AC = BC
... (i)
To Prove:
$AC = \frac{1}{2}AB$
Figure:
We can draw a figure to represent this situation:
Proof:
From the figure, we can see that the line segment AB is made up of two parts, AC and CB.
According to Euclid's axiom that states "things which coincide with one another are equal to one another", we can write:
AB = AC + CB
... (ii)
We are given from (i) that AC = BC.
We can substitute BC with AC in equation (ii):
$AB = AC + AC$
Now, we use Euclid's axiom that "things which are doubles of the same thing are equal to one another."
$AB = 2AC$
To solve for AC, we can divide both sides by 2.
$AC = \frac{1}{2}AB$
Hence, proved.
Question 5. In Question 4, point C is called a mid-point of line segment AB. Prove that every line segment has one and only one mid-point.
Answer:
Given:
A line segment AB.
To Prove:
The line segment AB has one and only one midpoint.
Proof:
We will prove this by contradiction.
Let's assume that the line segment AB has two distinct midpoints, which we will call C and D.
By the definition of a midpoint, if C is a midpoint of AB, then C lies between A and B, and:
$AC = \frac{1}{2}AB$
... (i)
Similarly, if D is also a midpoint of AB, then D lies between A and B, and:
$AD = \frac{1}{2}AB$
... (ii)
Now, we use Euclid's Axiom 1, which states: "Things which are equal to the same thing are equal to one another."
From equations (i) and (ii), since both AC and AD are equal to $\frac{1}{2}AB$, they must be equal to each other.
$AC = AD$
This equality can only be true if the points C and D are not distinct, but are in fact the same point. This is because, for two line segments starting from the same point A and lying on the same line, to have the same length, their endpoints (C and D) must coincide.
This contradicts our initial assumption that C and D are two distinct midpoints.
Therefore, our assumption was false, and a line segment cannot have more than one midpoint.
Hence, every line segment has one and only one midpoint.
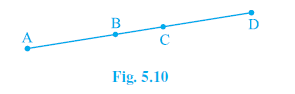
Question 6. In Fig. 5.10, if AC = BD, then prove that AB = CD.
Answer:
Given the arrangement of points A, B, C, D on a line as shown in Fig 5.10.
We are given the condition: $AC = BD$ (Equation 1)
From the figure, point B lies between A and C. By the Segment Addition Postulate:
$AC = AB + BC$ (Equation 2)
Also from the figure, point C lies between B and D. By the Segment Addition Postulate:
$BD = BC + CD$ (Equation 3)
Now substitute the expressions for AC (from Eq. 2) and BD (from Eq. 3) into the given Equation 1:
$AB + BC = BC + CD$
We have the length BC common to both sides of the equation.
According to Euclid's Axiom 3 ("If equals are subtracted from equals, the remainders are equal"), we can subtract BC from both sides:
$(AB + BC) - BC = (BC + CD) - BC$
Simplifying both sides gives:
$AB = CD$
Hence, proved.
Question 7. Why is Axiom 5, in the list of Euclid’s axioms, considered a ‘universal truth’? (Note that the question is not about the fifth postulate.)
Answer:
Euclid's Axiom 5 states: "The whole is greater than the part."
This axiom is considered a 'universal truth' because it is a self-evident and intuitive concept that holds true in all situations and fields of study, not just in geometry. It is a fundamental principle of logic and quantity that does not require any proof because it is obviously true by definition.
Here’s why it is considered a universal truth:
1. It is Self-Evident: The statement is inherently obvious. If you have a complete object (the whole) and you take a piece or a section of it (the part), the original object must be larger than the piece you took. For example, a whole cake is always bigger than a slice of that same cake.
2. It Applies Beyond Geometry: Unlike Euclid's postulates, which are specific to geometry, his axioms (or common notions) are principles that apply to all logical reasoning.
- In Arithmetic: The number 100 (the whole) is greater than 50 (a part of 100).
- In Geography: The area of a country (the whole) is greater than the area of any single state within it (the part).
- In everyday life: A full jug of water (the whole) contains more water than a glass of water poured from it (the part).
3. It is a Foundational Principle: Such universal truths are necessary starting points for building any logical system. Without accepting some basic, obvious truths without proof, we would be stuck in an endless loop of needing to prove every single statement, which is impossible. Axiom 5 is one such foundational block upon which mathematics is built.
As noted in the question, this is different from Euclid's Fifth Postulate (the parallel postulate), which is a more complex assumption specific to geometry and is not considered a simple, universal truth. Axiom 5, on the other hand, is accepted as true in any context imaginable.
Example 3 (Before Exercise 5.2)
Example 3. Consider the following statement: There exists a pair of straight lines that are everywhere equidistant from one another. Is this statement a direct consequence of Euclid’s fifth postulate? Explain.
Answer:
Solution:
The statement describes the existence of parallel lines. Parallel lines are defined as straight lines that are in the same plane and are everywhere equidistant from each other, meaning they never intersect.
Now, let's consider whether this statement is a direct consequence of Euclid's fifth postulate.
Euclid's Fifth Postulate:
"If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than two right angles."
In the diagram above, if $\angle 1 + \angle 2 < 180^\circ$, then lines m and n will eventually intersect on the right side.
Is the statement a direct consequence of the fifth postulate?
Yes, the statement is a direct consequence of Euclid's fifth postulate. Here's the explanation:
Euclid's fifth postulate tells us the condition under which two lines will intersect. By considering the opposite of this condition, we can deduce the condition under which two lines will not intersect, which is the definition of parallel lines.
Let's analyze the implication:
1. The fifth postulate states that if the sum of the interior angles on one side of the transversal is less than $180^\circ$, the lines meet on that side.
2. If the sum of the interior angles on one side is greater than $180^\circ$, then the sum on the other side must be less than $180^\circ$, so the lines would meet on the other side.
3. Therefore, the only way for the two lines not to meet on either side (i.e., to be parallel) is if the sum of the interior angles on one side is exactly equal to two right angles ($180^\circ$).
If $\angle 1 + \angle 2 = 180^\circ$, the lines will not intersect. This condition defines parallel lines.
So, the existence of a pair of lines that are everywhere equidistant (parallel) is guaranteed by the fifth postulate. The postulate gives us a specific condition ($\angle 1 + \angle 2 = 180^\circ$) under which parallel lines must exist.
In essence, the fifth postulate is what makes Euclidean geometry a "flat" geometry where parallel lines exist and behave in this predictable way. Without this postulate (or an equivalent one), we cannot guarantee the existence of such lines.
Exercise 5.2
Question 1. How would you rewrite Euclid’s fifth postulate so that it would be easier to understand?
Answer:
Euclid's fifth postulate is famously complex in its original wording. A simpler way to state its meaning is through an equivalent statement known as Playfair's Axiom.
Rewritten Version (Playfair's Axiom):
"For any given line and a point not on the line, there is exactly one line through the point that is parallel to the given line."
Explanation of why this is easier to understand:
- It's more direct and constructive: Instead of describing a condition for two lines to intersect (as Euclid's original postulate does), this version directly states a clear, positive fact about parallel lines. It tells you what you can draw.
- It uses a more familiar concept: The idea of "parallel lines" is more intuitive and commonly understood than "the sum of interior angles on the same side of a transversal."
- It's visually simpler: You can easily picture a line and a point not on it, and then imagine drawing another line through that point that will never meet the first one.
This rewritten version is logically equivalent to Euclid's fifth postulate within the framework of Euclidean geometry, but it is much more accessible and easier to grasp for most people.
Question 2. Does Euclid’s fifth postulate imply the existence of parallel lines? Explain.
Answer:
Yes, Euclid's fifth postulate directly implies the existence of parallel lines.
Explanation:
Euclid's fifth postulate provides the precise conditions under which two lines will intersect. By logical extension, it also defines the exact condition under which they will not intersect, which is the definition of parallel lines.
Here's a step-by-step explanation:
1. Recall the Postulate: The fifth postulate states that if a transversal line intersects two other lines, and the sum of the interior angles on one side is less than two right angles (180°), then the two lines will eventually meet on that side.
2. Consider the Condition for Intersection: The lines m and n intersect if $\angle 1 + \angle 2 < 180^\circ$.
3. Consider the Condition for Non-Intersection (Parallelism): The postulate implies that if the lines do not meet, then the condition for intersection must not be met. This means the sum of the interior angles cannot be less than 180°.
Similarly, if the sum on one side were greater than 180°, the sum on the other side would be less than 180°, and the lines would meet on that other side.
Therefore, the only way for the lines to never meet on either side is if the sum of the interior angles on one side is exactly equal to two right angles (180°).
$\angle 1 + \angle 2 = 180^\circ$
(Condition for parallel lines)
4. Conclusion: Because the fifth postulate specifies a condition where lines are guaranteed to meet, it simultaneously defines the one and only condition where they are guaranteed not to meet. This establishes the existence of parallel lines as a direct consequence of the postulate. Without this postulate, we could not be certain that such lines exist or that there is only one such line through a given point.

